
Voici les attendus des programmes en Français et mathématiques pour le niveau CM2
Ce ne sont que des repères qui permettent de savoir ce qu’un élève de CM2 doit avoir vu et acquis dans l’année. Ce ne sont que des repères et il est évident que l’enfant doit progresser à son rythme. Toutes les notions seront retravaillées en 6ème.
Français
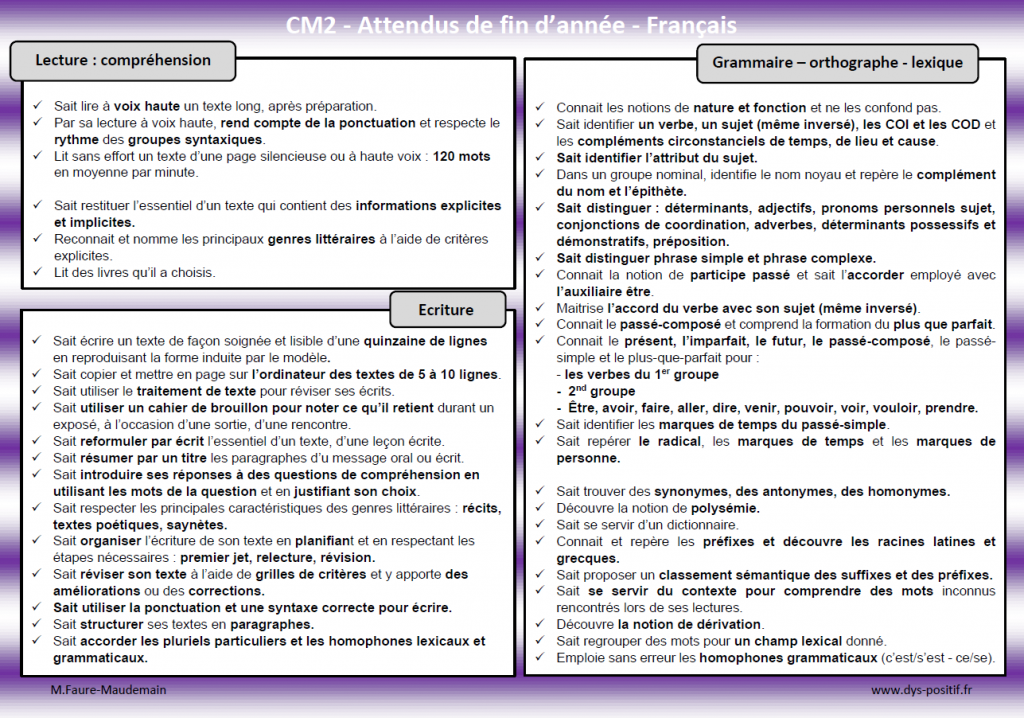
1- Lecture-compréhension
- Sait lire à voix haute un texte long, après préparation.
- Par sa lecture à voix haute, rend compte de la ponctuation et respecte le rythme des groupes syntaxiques.
- Lit sans effort un texte d’une page silencieuse ou à haute voix : 120 mots en moyenne par minute.
- Sait restituer l’essentiel d’un texte qui contient des informations explicites et implicites.
- Reconnait et nomme les principaux genres littéraires à l’aide de critères explicites.
- Lit des livres qu’il a choisis.
2- Lecture-écriture
- Sait écrire un texte de façon soignée et lisible d’une quinzaine de lignes en reproduisant la forme induite par le modèle.
- Sait copier et mettre en page sur l’ordinateur des textes de 5 à 10 lignes.
- Sait utiliser le traitement de texte pour réviser ses écrits.
- Sait utiliser un cahier de brouillon pour noter ce qu’il retient durant un exposé, à l’occasion d’une sortie, d’une rencontre.
- Sait reformuler par écrit l’essentiel d’un texte, d’une leçon écrite.
- Sait résumer par un titre les paragraphes d’u message oral ou écrit.
- Sait introduire ses réponses à des questions de compréhension en utilisant les mots de la question et en justifiant son choix.
- Sait respecter les principales caractéristiques des genres littéraires : récits, textes poétiques, saynètes.
- Sait organiser l’écriture de son texte en planifiant et en respectant les étapes nécessaires : premier jet, relecture, révision.
- Sait réviser son texte à l’aide de grilles de critères et y apporte des améliorations ou des corrections.
- Sait utiliser la ponctuation et une syntaxe correcte pour écrire.
- Sait structurer ses textes en paragraphes.
- Sait accorder les pluriels particuliers et les homophones lexicaux et grammaticaux.
3- Grammaire – orthographe – lexique
- Connait les notions de nature et fonction et ne les confond pas.
- Sait identifier un verbe, un sujet (même inversé), les COI et les COD et les compléments circonstanciels de temps, de lieu et cause.
- Sait identifier l’attribut du sujet.
- Dans un groupe nominal, identifie le nom noyau et repère le complément du nom et l’épithète.
- Sait distinguer : déterminants, adjectifs, pronoms personnels sujet, conjonctions de coordination, adverbes, déterminants possessifs et démonstratifs, préposition.
- Sait distinguer phrase simple et phrase complexe.
- Connait la notion de participe passé et sait l’accorder employé avec l’auxiliaire être.
- Maîtrise l’accord du verbe avec son sujet (même inversé).
- Connait le passé-composé et comprend la formation du plus que parfait.
- Connait le présent, l’imparfait, le futur, le passé-composé, le passé-simple et le plus-que-parfait pour :
- – les verbes du 1er groupe
- – 2nd groupe
- – Être, avoir, faire, aller, dire, venir, pouvoir, voir, vouloir, prendre.
- Sait identifier les marques de temps du passé-simple.
- Sait repérer le radical, les marques de temps et les marques de personne.
- Sait trouver des synonymes, des antonymes, des homonymes.
- Découvre la notion de polysémie.
- Sait se servir d’un dictionnaire.
- Connait et repère les préfixes et découvre les racines latines et grecques.
- Sait proposer un classement sémantique des suffixes et des préfixes.
- Sait se servir du contexte pour comprendre des mots inconnus rencontrés lors de ses lectures.
- Découvre la notion de dérivation.
- Sait regrouper des mots pour un champ lexical donné.
- Emploie sans erreur les homophones grammaticaux (c’est/s’est – ce/se).
Mathématiques
1- Nombres et calculs : les nombres entiers
- Sait utiliser et représenter les grands nombres entiers : Connait les unités, dizaines, centaines, milliers, millions, milliards et les relations qui les lient, comprend et applique les règles de la numération décimale de position aux grands nombres entiers (jusqu’à 12 chiffres).
- Sait comparer, ranger, encadrer des grands nombres entiers, les repérer et les placer sur une demi-droite graduée.
2- Nombres et calculs : les fractions
- Sait utiliser les fractions simples (comme 2/5 , ¼, 5/2) dans le cadre de partage de grandeurs ou de mesures de grandeurs et des fractions décimales (1/10 , 1/100) .Fait le lien entre /2 et « la moitié de.. »).
- Sait manipuler les fractions jusqu’à 1/1000.
- Connait les désignations des fractions : orales, écrites et des décompositions additives et multiplicatives (ex 4/3 = 1/3+1/3+1/3+1/3 = 1+1/3 = 4×1/3).
- Sait positionner les fractions sur une droite graduée.
- Encadre les fractions entre deux nombres consécutifs.
- Sait écrire une fraction sous forme de somme d’un entier et d’une fraction inférieure à 1.
- Sait comparer deux fractions de même dénominateur.
- Connait les égalités entre des fractions usuelles (par ex : 5/10 = ½ = 10/100 = 1/10 ou 2/4 = ½).
3- Nombres et calculs : organisation et gestion des données
- Sait prélever des données numériques à partir de supports variés. Il produit des tableaux, des diagrammes et des graphiques pour organiser les données numériques.
- Sait lire et construire des tableaux, diagrammes en bâtons ou circulaires, semi-circulaire et des graphiques.
4- Nombres et calculs : résoudre des problèmes
- Sait résoudre des problèmes nécessitant l’emploi de l’addition ou de la soustraction (jusqu’au milliard et avec les décimaux jusqu’à trois décimales).
- Sait résoudre des problèmes faisant intervenir la multiplication ou la division.
- Sait résoudre des problèmes nécessitant une ou plusieurs étapes.
- Sait résoudre des problèmes relevant de la proportionnalité.
5- Nombres et calculs : calcul mental
- Connait et a mémorisé les premiers multiples de 25 et de 50.
- Sait multiplier par 5,10, 50 et 100 les nombres décimaux.
- Sait diviser par 10 et 100 les nombres décimaux.
- Connait les compléments au nombre entier supérieur (12+199 = 200+12 -1 = 212-1).
- Connait les critères de divisibilité par 2, 3, 5, 9 et 10.
- Sait estimer un ordre de grandeur.
6- Nombres et calculs : les nombres décimaux
- Connait les unités de la numération décimale (unités simples, dixièmes, centièmes, millièmes) et les relations qui les lient.
- Connait la valeur des chiffres en fonction de leur rang.
- Sait utiliser les nombres décimaux pour rendre compte de mesures de grandeurs : connait le lien entre les unités de numération et unités de mesure (dixième →dm,dg,dl ou centième → cm, cg, cl, centimes d’euro.
- Sait repérer et placer un nombre décimal sur une demi-droite graduée.
- Sait comparer et ranger les nombres décimaux.
- Sait encadrer un nombre décimal par deux nombres entiers, par deux nombres décimaux ;
- Sait trouver des nombres décimaux à intercaler entre deux nombres donnés.
7- Nombres et calculs : calcul posé
- Sait poser et calculer des additions en colonnes (sur les nombres inférieurs à 1 000).
- Sait poser et calculer des soustractions en colonne (sur les nombres inférieurs à 1000).
- Sait poser et calculer des multiplications.
- Sait poser et calculer des additions et des soustractions de nombres décimaux.
- Sait poser des multiplications d’un nombre décimal par un nombre entier.
- Sait poser une division euclidienne de deux nombres entiers : quotient décimal ou pas (10/4 ; 10/3 …).
- Sait poser des divisions d’un nombre décimal par un nombre entier.
8- Problèmes impliquant des grandeurs
- Sait calculer des périmètres, des aires et des volumes en mobilisant ou non des formules donnant : le périmètre d’un carré, d’un rectangle ; L’aire d’un carré, d’un rectangle.
- Calcule la durée écoulée entre deux instants donnés.
- Détermine un instant à partir de la connaissance d’un instant et d’une durée.
- Connait les unités de mesures usuelles : jour, semaine, heure, minute, seconde, dixième de seconde, mois, année, siècle, millénaire.
- Résout des problèmes en exploitant des ressources variées (horaires de transport, horaires de marées, programme de cinéma ou de télévision).
- Identifie une situation de proportionnalité entre deux grandeurs à partir du sens de la situation. Des situations s impliquant des échelles et des vitesses constantes peuvent être rencontrées.
9- Grandeurs et mesures
Longueurs :
- Compare des périmètres
- Mesure des périmètres par report d’unités ou de fractions d’unités ou par report des longueurs des côtés sur un segment de droite avec le compas.
- Calcule le périmètre d’un polygone en ajoutant les longueurs de ses côtés.
- Sait établir les formules du périmètre du carré et du rectangle, puis les utilise.
Aires :
- Comparer des surfaces selon leur aire.
- Différencie aire et périmètre d’une figure.
- Détermine ou estime une aire en faisant appel à une aire de
- Utilise systématiquement une unité de référence : cm², dm², le m².
- Utilise les formules d’aire du carré et du rectangle.
Dates et durées :
- Consolide la lecture de l’heure.
- Réalise des conversions : siècle/années ; semaine/jours ; heure/minutes ; minute/secondes.
- Réalise des conversions nécessitant l’interprétation d’un reste : transformer des heures en jours, avec un reste en heures ou des secondes en minutes, avec un reste en secondes.
Contenances :
- Découvre qu’un litre est la contenance d’un cube de 10cm d’arête.
- Relie des unités de volume et de contenance.
- Estime la mesure d’un volume ou d’une contenance et l’exprime dans une unité adaptée : cm3, dm3, m3.
- Utilise de nouvelles unités de contenance : dL, cL et mL.
Angles :
- Identifie les angles d’une figure plane, puis compare ces angles par superposition, avec du papier calque ou un gabarit.
- Estime puis vérifie en utilisant l’équerre qu’un angle est droit, obtus ou aigus.
- Construit un angle droit à l’aide de l’équerre.
10- Espace et géométrie
- Se repérer et se déplacer dans l’espace en utilisant ou en élaborant des représentations : Se repère, décrit ou exécute des déplacements sur un plan ou sur une carte (école, quartier ville, village); décrit et code des déplacements dans des espaces familiers; il programme les déplacements d’un robot ou ceux d’un personnage sur écran; connait le vocabulaire permettant de définir des positons ou des déplacements (à gauche ; à droite, faire demi-tour, effectuer un quart de tout à droite, à gauche); réalise divers modes de représentation de l’espace : maquettes, plans, schémas.
- Reconnait, nomme et décrit des figures simples et complexes :
- Triangle rectangle, triangle isocèle, triangle équilatéral.
- Quadrilatères : carré, rectangle, losange, première approche du parallélogramme.
- Cercle disque.
- Reconnait, nomme et décrit des solides simples : cube, pavé droit, prisme droit, pyramide, cylindre, cône, boule.
- Connait le vocabulaire associé aux objets et aux priorités : côté, sommet, angle, diagonale, polygone, centre, rayon, diamètre, milieu, hauteur, solide, face, arête.
- Sait reproduire, représenter et construire : des patrons différents pour un cube de dimension donnée.
- Reconnait les patrons : d’un cube, d’un pavé droit et d’une pyramide.
- Il réalise, complète et rédige un programme de construction.
- Réalise une figure simple ou composée de figure simples à l’aide d’un logiciel.
- Connait les notions d’alignement/appartenance, de perpendicularité/parallélisme, de segment de droite, de distance entre deux points, entre un point et une droite.
- Sait tracer avec l’équerre la droite perpendiculaire à une droite donnée passant par un point donné qui peut être extérieur à la droite.
- Sait tracer avec la règle et l’équerre la droite parallèle à une droite donnée passant par un point et une droite.
- Sait tracer un carré, un rectangle, un triangle rectangle de dimensions données.
- Sait observer que deux points sont symétriques par rapport à une droite donnée lorsque le segment qui les joint coupe cette droite perpendiculairement en son milieu.
- Sait construire, à l’équerre et à la règle graduée, le symétrique par rapport à une droite d’un point, d’un segment, d’une figure.
